Matematikdelen  side 13

Mere om cosh(x)

Hyperbolske funktioner og kædelinier

Her kræves kendskab til differential- og integralregning.

Definition (h1):

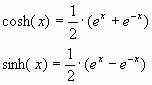
Differentiabilitet (h2):

sinh(x) og cosh(x) er differentiable og

Ovenstående bevises let ved at betragte definitionerne.

Man får af (h2) at:

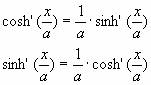
Andre egenskaber

En anden egenskab der også minder om egenskaber ved de trigonometriske funktioner er:

 Dette vises ved at bruge definitionerne og indse at

Funktionsfamilien

har alle globalt minimum i x=0 med minimumsværdien a.

Dette ses ved at løse f´(x)=sinh(x/a)=0 hvor man får x=0 og da sinh(x/a) er negativ for x<0 og positiv for x>0 fås at x=0 er et globalt minimumssted og at minimumsværdien er f(0)=a.

Ligeledes ses det af definitionen på cosh(x) at

så de tilhørende kurver har alle anden-aksen som symmetriakse.

Længden af en kædelinie

I forbindelse med bestemmelse af kædelinien ud fra længden l af buen bruger vi følgende sammenhæng:

 Dette kan bevises ved at bruge en velkendt sætning som vi anfører uden bevis. Beviset kan f.eks. findes på side 50 i Højniveaumatematik 2, Thomas Hebsgaard et al. Herfra fås:

 hvor f er en differentiabel funktion og l er længden af grafen.

Vi får nu ved at indsætte

som f(x):

 hvor vi integrerer fra x=-r til x=r , bruger at

er symmetrisk omkring 2.-aksen og bruger (h1), (h2) og (h3). Idet r er x-værdien vi bruger til endepunktet på buen, har vi det ønskede og overraskende resultat, at længden af kædelinien for funktionen

fra  x=0 er givet ved

.