Fysikken bag kædelinien    side 15

Fysikken bag kædelinien
 

Her kræves kendskab til differential- og integralregning.

Problemet vedrørende kædelinien går ud på at finde den kurve som en kæde danner når den er udspændt mellem to punkter. Leonardo da Vinci og Galilei havde studeret kurven og sidstnævnte mente at kurven var en parabel. Johan Bernoulli løste problemet ved at bruge differentialregning og vi vil nu se lidt nærmere på hvordan man kan løse problemet.

Figuren nedenfor viser en kæde der er ophængt i to punkter. Kæden er fuldstændig bøjelig og uelastisk. Koordinatsystemet placeres således at kædens laveste punkt ligger på y-aksen i A(0,a).

Tallet a er bestemt af kædens masse pr. længdeenhed, tyngdeaccelerationen og de vandrette trækkræfters størrelse. Vi vil bestemme en regneforskrift for den kurve (kædelinien) kæden danner ved at betragte de trækkræfter der påvirker kæden i A og i et tilfældigt punkt B(x,y) på kædelinien.
 

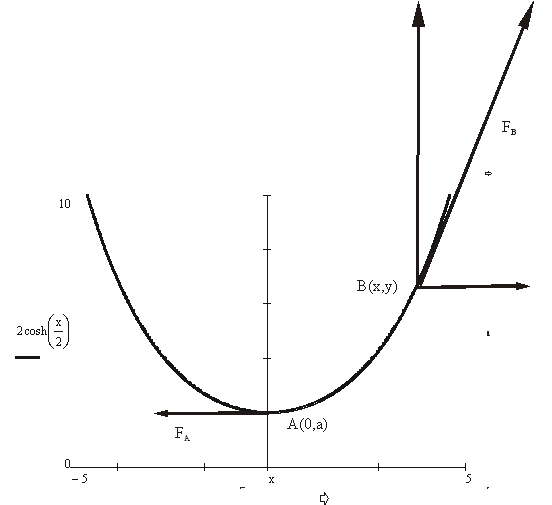
  Kæden mellem A og B er påvirket af tyngdekraften Ft og de to trækkræfter FA og FB.
  Da FA og FB begge peger i tangentens retning, kan de opskrives på følgende måde:

           og

hvor k0 og k1 er konstanter. Tyngdekraften Ft virker nedad og er givet ved

hvor m er massen af kæden mellem A og B. Hvis massen pr. længdeenhed kaldes µ kan massen m bestemmes:

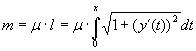
hvor længden af kurven l er givet ved det samme integral som vi betragtede i forbindelse med længden af kædelinien.

Da kæden er i hvile er den resulterende kraft lig med 0, dvs. at

          ++=

Heraf fås at:

          ++=

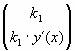Vi får nu at k1 = k0 og at

          =

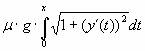
Differentieres denne ligning fås

hvor , dvs. c er en konstant.

Dette er en differentialligning der kan løses mht. y´(x) ved brug af separation af de variable. Vi sætter z=y´ og får:

Man får

Idet z(0)=y´(0)=0 er c1=0 så

Man får så:

dvs.

som jo er en velkendt funktion. En stamfunktion findes nu let så

Løsningskurven der går gennem (0,a) har

 og

 Indsættes a fås løsningen